Path instability of falling permeable disks
From the dispersal of dandelion seeds carried by the wind to phytoplankton settling in the ocean, predicting bifurcations resulting from fluid–solid interactions on a freely falling object is an intriguing subject. Its applications span across meteorology, ecology, insect flight, and engineering. The literature extensively explores the interactions between wake and free-fall dynamics. Common objects like paper sheets exhibit diverse falling paths, including fluttering and tumbling trajectories. Similar zig-zag and oblique paths are observed for buoyant drops and bubbles. Buoyancy-driven disks hold significant interest in fluid dynamics due to their varied falling paths, such as zig-zag, tumbling, and chaotic motion. In the case of disks with very small thickness, a relatively larger flow inertia leads to a transition from a steady vertical (SV) path to a zig-zag regime. This is characterized by very low-amplitude oscillations at low values of disk inertia and large-amplitude oscillations at moderate to large disk inertia. Authors observed, for a thickness-to-diameter ratio of 0.1, a transition from the SV path to a regime characterized by a steady oblique trajectory with a constant disk inclination. This is analogous to findings by Fabre, Tchoufag & Magnaudet (2012) through a weakly nonlinear expansion around the SV path. However, direct numerical simulations face challenges due to their high computational cost, particularly in parametric studies. The temporal transient becomes (virtually) infinitely long near instability thresholds. From this perspective, a suitable approach to address large parametric studies and obtain precise thresholds is linear stability analysis. This tool provides the threshold value of the instability of a certain path concerning perturbations, as well as detailed information about the unstable neutral mode, within a reasonable computational time. As a consequence of linearizing the governing equations, linear stability analysis allows us to understand the emerging path only in the vicinity of the instability threshold and does not provide information on the nonlinear saturated state. Several falling objects, such as dandelions, are known to possess permeable structures (Cummins et al. 2018). Permeable disks serve as a suitable testing ground to investigate the role of permeability in modifying the trajectories of thin bodies. For this purpose, the combination of linear stability analysis and the homogenized model is appropriate for conducting a parametric study and gaining a comprehensive understanding of the path instability of a thin buoyancy-driven permeable disk. The employed formalism allows us to obtain general results, independent of a specific microscopic structure.
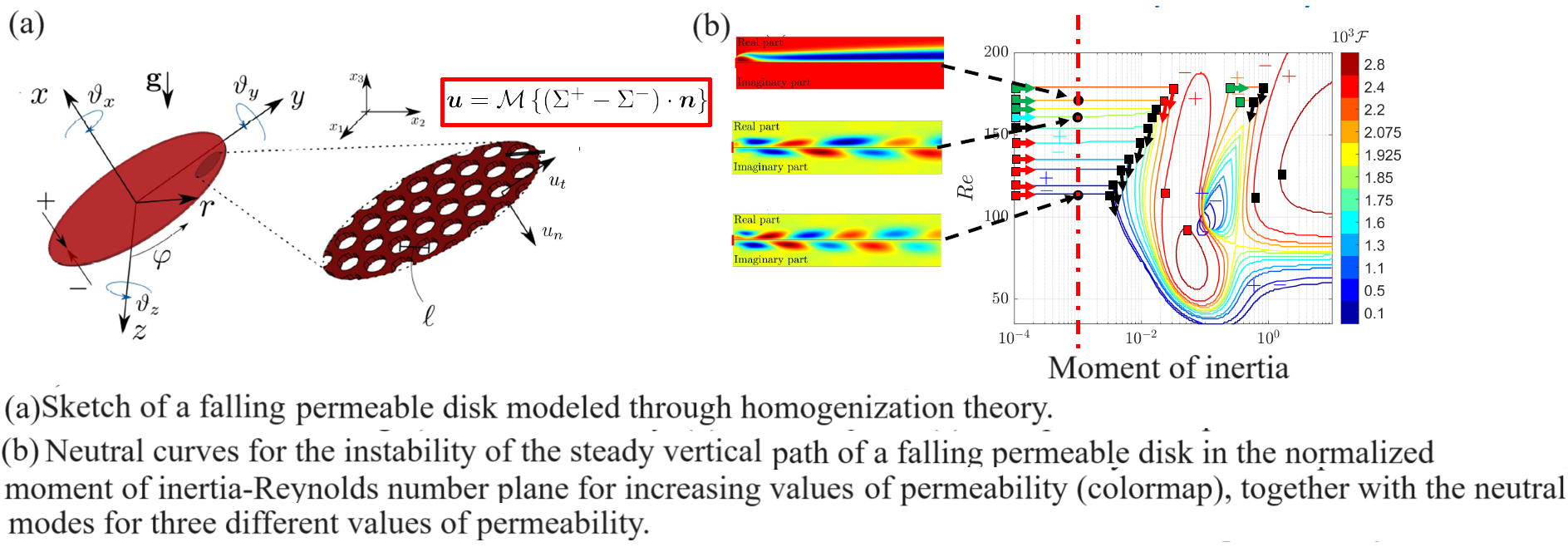
Therefore, with the aim of uncovering the modifications induced by permeability to the intricate instabilities characterizing the ascent or descent of a buoyancy-driven thin disk, we perform a linear stability analysis of the SV path concerning azimuthal perturbations of a disk modeled as a thin permeable membrane. We predict the values of parameters ensuring a stable, steady vertical path and the emergence of unstable trajectories. In the linear stability analysis of the steady vertical path of a thin permeable disk, whose flow through the microstructure is modeled using a stress-jump model based on homogenization theory, the relative velocity of the flow associated with the vertical steady path reveals a recirculation region detached from the body. This region shrinks and eventually disappears as the disk becomes more permeable. In analogy with the solid disk, one non-oscillatory and several oscillatory modes are identified, destabilizing the fluid–solid coupled system away from its straight trajectory. Permeability progressively filters out wake dynamics in the instability of the steady vertical path. Modes dominated by wake oscillations are initially stabilized, followed by those characterized by weaker or absent wake oscillations, where the wake typically involves tilting induced by the disk's inclined trajectory. For sufficiently large permeabilities, the disk first experiences a non-oscillatory divergence instability, expected to result in a steady oblique path with a constant disk inclination in the nonlinear regime. Further increases in permeability reduce the unstable range of all modes until the quenching of all linear instabilities. In collaboration with the group led by Prof. A. De Simone, within the iSeed project framework (https://iseedproject.eu/), we are performing a similar analysis on perforated disks, with the aim of highlighting relevant behaviors for environmental monitoring.